Zoeken - zoekresultaten
verfijn de resultaten
Eigenschappen van de optelling
Bij optellen gaat het om samenvoegen of toevoegen van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van de optelling zijn bijvoorbeeld:
- de verwisseleigenschap van de optelling: 3 + 4 = 4 + 3
- de volgorde bij het optellen doet er niet toe: 8 + 6 = 8 + (2 + 4). Dat gebruik je bijvoorbeeld bij de splitsing bij de tien, 8 + (2 + 4) wordt dan (8 + 2) + 4 en dan doe je eerst 8 + 2 = 10 en dan 10 + 4 = 14
- 9 + 7 = 10 + 6 of 10 + 7 - 1 (ééntje méér, ééntje minder)
Eigenschappen van de aftrekking
Bij aftrekkingen gaat het om het verminderen of het bepalen van verschil van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van het aftrekken zijn bijvoorbeeld:
- een aftrekking mag je niet omkeren: 7 - 4 ≠ 4 - 7
- de volgorde doet er wel toe: (6 - 3) + 2 ≠ 6 - (3 + 2)
- 15 - 9 = 16 - 10 of 15 - 10 + 1 (ééntje meer, ééntje minder)
Eigenschappen van de vermenigvuldiging
Bij vermenigvuldigingen gaat het om herhalingen, zoals vier groepjes van 5, vier staafjes van 5, vier sprongen van 5. Of "vier keer (telkens) 5".
Belangrijke eigenschappen van het vermenigvuldigen zijn bijvoorbeeld:
- een vermenigvuldiging mag je verwisselen: 3 x 12 = 12 x 3
- de volgorde bij het vermenigvuldigen doet er niet toe: 6 x 24 = (2 x 3) x 24 = 2 x (3 x 24) = 2 x 72 = 144
- vermenigvuldigen met 10 is gemakkelijk: 10 x 256 = (256 tientallen) = 2560. Alles schuift een positie op, of kort gezegd: je zet er een nul achter.
- 6 x 99 = 6 x 100 - 6 x 1 (één keer meer, één keer minder)
- 8 x 25 = 4 x 50 (verdubbelen en halveren)
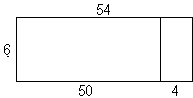
- de verdeeleigenschap: 6 x 54 = 6 x 50 + 6 x 4, zoals in het onderstaande oppervlaktemodel te zien is.
Eigenschappen van de deling
Bij verdelen kan het gaan om verdelen (Van een banketstaaf van 25 cm snijden we stukjes van 3 cm. Hoeveel stukjes kunnen we maken?) en opdelen (in een kring van vier kinderen delen we 20 kaartjes uit door telkens een rondje te geven. Hoeveel krijgt ieder?).
Belangrijke eigenschappen van het delen zijn bijvoorbeeld:
- een deling mag je niet omkeren: 12 : 3 ≠ 3 : 12
- bij een deling doet de volgorde er wel toe: (24 : 6) : 2 ≠ 24 : (6 : 2)
- delen door 10 is gemakkelijk. 2340 : 10 = (hoeveel tientallen zitten er in 2340) = 234. Je mag er een nul afhalen.
- bij een deling geldt ook de verdeeleigenschap: 64 : 4 = 40 : 4 + 24 : 4
De activiteiten in groep 3/4 bouwen voort op die in groep 1/2: leerlingen breiden hun kennis (wat is waar te vinden) en hun vaardigheden (je weg vinden in het aanbod en bronnen) uit. Leerlingen maken kennis met de functie en opzet van verschillende informatiebronnen zoals een woordenboek of een tijdschrift.
Kerndoel 1
De leerlingen leren zich mondeling en schriftelijk begrijpelijk uit te drukken.
Kerndoel 2
De leerlingen leren zich te houden aan conventies (spelling, grammaticaal correcte zinnen, woordgebruik) en leren het belang van die conventies te zien.
Kerndoel 3
De leerlingen leren strategieën te gebruiken voor het uitbreiden van hun woordenschat.
Kerndoel 4
De leerlingen leren strategieën te gebruiken bij het verwerven van informatie uit gesproken en geschreven teksten.
Kerndoel 6
De leerlingen leren deel te nemen aan overleg, planning en discussie in een groep.
Kerndoel 7
De leerlingen leren een mondelinge presentatie te geven.
Kerndoel 9
De leerlingen leren taalactiviteiten (spreken, luisteren, schrijven en lezen) planmatig voor te bereiden en uit te voeren.
Kerndoel 10
De leerlingen leren te reflecteren op de manier waarop zij hun taalactiviteiten uitvoeren en leren, op grond daarvan en van reacties van anderen, conclusies te trekken voor het uitvoeren van nieuwe taalactiviteiten.
De fragmenten van gesprekken waarin leerlingen iets vertellen over de materiële leesomgeving thuis laten zien dat dergelijke informatie waardevol inzicht kan geven in hoe er thuis gelezen wordt en of kinderen daarin gestimuleerd worden.