Rekenen/wiskunde - Getallen en bewerkingen - kerndoel 26
De leerlingen leren structuur en samenhang van aantallen, gehele getallen, kommagetallen, breuken, procenten en verhoudingen op hoofdlijnen te doorzien en er in praktische situaties mee te rekenen.
Toelichting en verantwoording
hoeveelheden, groottes en hun relaties Van toepassing voor: groep 1 en 2; groep 3 en 4; groep 5 en 6; groep 7 en 8;
Inhoud voor: groep 1 en 2
- (kleine) hoeveelheden vergelijken (méér, minder evenveel)
- hoeveelheden tellen (resultatief tellen)
- meten door afpassen
- benoemde hoeveelheden, groottes, data etc. (waarvan je de getallen weet) vergelijken op grond van die getallen.
Bijvoorbeeld bij een vraag als "wie is het oudst?"
- getallen met elkaar vergelijken op basis van volgorde in de telrij en door vergelijking van corresponderende hoeveelheden
- kleine hoeveelheden direct overzien
- getalpatronen herkennen, zoals die op de dobbelsteen en bij dominostenen
Inhoud voor: groep 3 en 4
als groep 1/2 +
- gestructureerde hoeveelheden en aantallen tellen (telstrategieën) en vergelijken
- aantallen tellen en vergelijken door die aantallen te structureren, zoals bij verpakkingen
- zie ook meten (kerndoel 33)
- getalpatronen op het vijfrek, kralenketting, honderdveld, wisselmateriaal (MAB)
- andere alledaagse getalpatronen, zoals: zes eieren in een doosje, vijf twintigjes in een euro, 12 in een dozijn
- even en oneven als eigenschap van getallen
Inhoud voor: groep 5 en 6
als groep 3/4 +
- hoeveelheden bepalen of vergelijken of tellen door bijvoorbeeld wegen (Wat zijn de meest erwten?) en meten (Waar liggen de meeste stenen?)
- zie ook meten (kerndoel 33)
- bijzondere getalpatronen: tafelgetallen op de getallenlijn en het honderdveld
Inhoud voor: groep 7 en 8
als in groep 5/6 +
- hoeveelheid bij benadering tellen of meten door middel van steekproeven
- het beredeneren van aantallen of grootte uit gegevens, zoals: een winkelier heeft 2,65 kg euromunten. Eén euromunt weegt volgens de bank 7,50 gram. Hoeveel munten zijn dat? Bij nátellen blijken het er 355 te zijn. Hoe kun je dat verklaren?
- zie ook meten (kerndoel 33)
- bijzondere getallen, zoals kwadraten, gemene veelvouden, delers en priemgetallen
structuur van de telrij en getalstructuur Van toepassing voor: groep 1 en 2; groep 3 en 4; groep 5 en 6; groep 7 en 8;
Inhoud voor: groep 1 en 2
- de telrij tot 10 / 20: de telwoorden, verder tellen en terugtellen vanaf een willekeurig getal
- telrij tot 100 (in oriënterende zin)
- aantallen en hoeveelheden structureren in tweetallen, vijftallen en tientallen en naar analogie van de vingers van twee handen de vijf- en tienstructuur: 0, 5, 10, 15, 20
Inhoud voor: groep 3 en 4
als groep 1/2 +
- de telrij tot 100 / 1.000
- tellen in sprongen van 2, 5 en 10
- positioneren van getallen in de telrij (bijvoorbeeld tussen twee tientallen) en op de (lege) getallenlijn
- ankergetallen in de telrij verkennen: Deze ankergetallen spelen een belangrijke rol bij het handig uitvoeren van de basisbewerkingen tot 100
- 5, 10, 15, 20, ...
- 10, 20, 30, ...
- 20, 40, 60, 80, 100, ...
- 25, 50, 75, 100
- hoeveelheden en getallen tot 100 structureren in tientallen, vijftallen en eenheden (Structuur van geld, rekenrek, kralenketting, honderdveld) en andere praktisch belangrijke structureringen zoals zestallen en twaalftallen
- aantallen en getallen structureren zoals: getalsplitsingen, verdubbelen/halveren, verschil tussen getallen kunnen bepalen
- relaties tussen ankergetallen en tijden van de klok: 4 kwartier in een uur, 60 minuten in een uur, 60 seconden in een minuut
- de indeling van geld (euro): 1, 2, 5, 10; 20, 50, 100
Inhoud voor: groep 5 en 6
als groep 3/4 +
- de telrij tot 1.000 / 100.000
- tellen in honderdvouden, duizendvouden etc.
- positioneren van getallen op de lege getallenlijn
- orde van grootte van getallen aangeven en vergelijken
(1.000 is echt klein ten opzichte van 100.000; of 7.850 ligt tussen 5.000 en 10.000, op zo'n dikke 2.000 afstand van 10.000 en op zo'n 3.000 afstand van 5.000)
- meer ankergetallen leren in de telrij: zoals
- 10, 100, 1000, ...
- 200, 400, 600, 800, 1000, ...
- 250, 500, 750, 1000
- en evenzo in het gebied van de duizendtallen en groter
- grote getallen structureren
- grote getallen positiegewijs onderling vergelijken
- grote getallen vergelijken met ankergetallen en referentiegetallen
- klokgetallen leren gebruiken, die cyclisch zijn: ná 24 (of 12), en ná 60 begin je met een nieuw(e) dag(deel), uur of minuut
- romeinse getallen (afgeleid van de vijfstructuur: 5, 10, 50, 100, etc.) verkennen
Inhoud voor: groep 7 en 8
als in groep 5/6 +
- tellen tot in miljoenen en miljarden
- afronden van getallen; nauwkeurigheid van afronden; nauwkeurigheid van getallen
- negatieve getallen (thermometer)
- termen om getalgrootte aan te geven: zoals kilo-, mega-, giga-, mili-, en micro-
- grote ankergetallen als referentiegetallen
- kennis van het talstelsel gebruiken bij het veranderen van maat, zoals bij 150 centimeter is 1,5 meter of bij 10.000 meter is hetzelfde als 10 kilometer
- tweetallig talstelsel (computer)
inzicht in de bewerkingen met gehele getallen Van toepassing voor: groep 1 en 2; groep 3 en 4; groep 5 en 6; groep 7 en 8;
Inhoud voor: groep 1 en 2
- betekenis van het resultatief tellen
- betekenis van het samenvoegen, doortellen, terugtellen, wegnemen, verschil bepalen in betekenisvolle situaties
Inhoud voor: groep 3 en 4
als groep 1/2 +
- betekenis van de bewerkingen optellen en aftrekken en verschillen bepalen in verschillende eenvoudige contexten
- verkenning van de eigenschappen van optellen en aftrekken
- verkenning van (de betekenis van) het vermenigvuldigen als basis voor kerndoel 27: het vlot kennen van de basisbewerkingen
Inhoud voor: groep 5 en 6
als groep 3/4 +
- betekenis van de bewerkingen vermenigvuldigen en delen in verschillende eenvoudige contexten
- verkenning van de eigenschappen van vermenigvuldigen en delen
- veelvouden en deelbaarheid als basis voor:
- kerndoel 27: het vlot kennen van de basisbewerkingen
- kerndoel 28: het schattend rekenen
- kerndoel 29: het handig rekenen
- kerndoel 30: het schriftelijk rekenen
- kerndoel 31: het gebruik van de rekenmachine
Inhoud voor: groep 7 en 8
als in groep 5/6 +
- uitbreiding van betekenis van de basisbewerkingen in:
- allerlei praktische contexten
- het rekenen met kommagetallen
- het meten en rekenen met maten
- meetkunde, zoals het vergroten / verkleinen van figuren
- fundamentele uitbreiding van betekenis van de basisbewerkingen in het rekenen met verhoudingen, procenten en breuken
kommagetallen, hun structuur en hun relaties Van toepassing voor: groep 5 en 6; groep 7 en 8;
Inhoud voor: groep 5 en 6
- begrip van kommagetallen vanuit:
- geld, zoals bij € 23,67
- maatverfijning (kerndoel 33), zoals bij 1,45 meter
- uitbreiding van het talstelsel, door rechts naast de komma posities te maken die telkens een tien keer zo kleine waarde hebben
- kommagetallen op de getallenlijn, door de ruimte tussen twee opeenvolgende hele getallen in tien stukjes te verdelen en zo verder
- getallen en kommagetallen met elkaar vergelijken op grond van het aantal cijfers, de plaats van de komma (positiewaarden) en de positiewaarden van de cijfers in de getallen
Inhoud voor: groep 7 en 8
als in groep 5/6 +
- redeneren over nauwkeurigheid van kommagetallen (maatgetallen), zoals bij:
- waarom staat op een melkpak soms 1000 ml een soms 1l e?
- wat betekent 1,65 miljoen en waarom schrijft men niet 1.650.000?
- verband tussen positiewaarden van cijfers in kommagetallen en het metriek stelsel
- samengestelde bewerkingen
- rekenregels, zoals bij het werken met haakjes en de volgorde van bewerkingen
breuken, hun structuur en hun relaties Van toepassing voor: groep 3 en 4; groep 5 en 6; groep 7 en 8;
Inhoud voor: groep 3 en 4
- half en kwart (onder andere in relatie tot boterhammen, een appel, uur, fles frisdrank)
Inhoud voor: groep 5 en 6
- breuken: verdelen in halven, kwarten, vijfden, achtsten, tienden, derden en zesden
- het plaatsen van breuken op de getallenlijn tussen de hele getallen.ook als gemengd getal
- breuk als operator, zoals bij 'een kwart van de Nederlanders'
- breuk als beschrijver van een deel van een geheel (een kwart taart), bij kleine en grote aantallen en hoeveelheden
- breuk als beschrijving van een verhouding (1 op de 3 Nederlanders, 1/3 van de Nederlanders)
- breuk als (reken)getal
- vergelijken van breuken (met stroken of breukenstokken) of van breuken als verhouding met verschillende redeneringen
- breuk als beschrijving van een eerlijke verdeling (2 pizza's verdelen met z'n drieën, dus ieder 2/3 pizza)
- indeling van breuken in klassen van gelijkwaardige breuken:
Inhoud voor: groep 7 en 8
als in groep 5/6 +
- verkennen van klassen van gelijkwaardige breuken; de eenvoudigste breuk uit een klasse
- vergelijken en ordenen van breuken
- vergelijken van eenvoudige en veel voorkomende breuken en kommagetallen
- omzetten van breuken in kommagetallen en omgekeerd
percentages Van toepassing voor: groep 7 en 8;
Inhoud voor: groep 7 en 8
- leren van de verschillende beschrijvingswijzen met een percentage:
- percentage als bijzondere breuk: 50% is de helft
- percentage als breuk met noemer 100: 1% =
- percentage als operator (35% van een aantal nemen)
- percentage als kommagetal: 75% = 0,75
- percentage in specifieke contexten, zoals winst, korting, rente of helling
- percentages in breuken omzetten en andersom, zoals bij 50% = 0,5 en
- diverse rekenstrategieën waaronder in ieder geval de 1% regel
verhoudingen, hun structuur en hun relaties Van toepassing voor: groep 3 en 4; groep 5 en 6; groep 7 en 8;
Inhoud voor: groep 3 en 4
- tafels van vermenigvuldiging als verhoudingstabel
- vergroten / verkleinen van figuren
- verhouding van bijvoorbeeld aantal en prijs
- verhoudingen in recepten
- verhoudingen met eenvoudige schaallijnen
Inhoud voor: groep 5 en 6
als in groep 3/4 +
- verhoudingen bij / als:
- schaal (verhoudingen)
- rekenen met snelheid, prijs per stuk of per verpakking, per gewicht
- berekeningen aan de hand van een plattegrond
- mengsels en recepten
- verhoudingen en verhoudingentaal
(1 op 5)
- gebruik van de verhoudingstabel
Inhoud voor: groep 7 en 8
als in groep 5/6 +
- omzetten van verhoudingen in breuken en percentages en andersom
- verhoudingen bij recepten en als vergrotingsfactor bij bijvoorbeeld figuren / kopiëren, foto's, dia's, digitale beelden op de computer
- verband tussen breuken en verhoudingen. Verhoudingen vergelijken / naar verhouding vergelijken
rekenen met breuken, procenten en verhoudingen Van toepassing voor: groep 7 en 8;
Inhoud voor: groep 7 en 8
- inzichtelijk rekenen met breuken:
- toepassen van de breuk als operator in betekenisvolle situaties: zoals bij 3/4 van de kinderen van de klas
- optellen en aftrekken van (gelijknamige en ongelijknamige) eenvoudige breuken (benoemd en onbenoemd=rekengetal)
- vermenigvuldigen van breuken met hele getallen ( 3/4 van 20,
3/4 x 20) en in betekenisvolle contexten met eenvoudige breuken
- veelvoud van een breuk berekenen (20 x 3/4)
- delen door (benoemde) breuken met behulp van verhoudingstabel (hoeveel glazen van 1/8 liter uit een fles van 1 liter?), voornamelijk in context
- rekenen met percentages als breuk en als kommagetal, eventueel met gebruik van o.a. verhoudingstabellen en de 1% regel
- rekenen met verhoudingen met behulp van verhoudingstabellen en met de dubbele getallenlijn
betekenissen en functies van getallen, breuken, verhoudingen, percentages, en hun onderling verband Van toepassing voor: groep 1 en 2; groep 3 en 4; groep 5 en 6; groep 7 en 8;
Inhoud voor: groep 1 en 2
- het onderscheiden van verschillende betekenissen van getallen bij het benoemen van onder andere aantallen, posities (de derde in de rij, huisnummers), tijd, leeftijd, gewicht, lengte, prijzen, kledingmaten en andere groottes
Inhoud voor: groep 3 en 4
als groep 1/2 +
- het onderscheiden van verschillende betekenissen van getallen bij:
- gebruik van getallen als hoeveelheidgetal (resultatief tellen) en het rekenen daarmee
- gebruik van getallen op de klok, de kalender, maatgetallen op meetlat en liniaal, getallen op de weegschaal, tijd en data, leeftijd, waarde (prijs, kosten), gewicht en temperatuur
- gebruik van getallen in allerlei (con)texten, zoals: de krant, de winkel, kledingmaten, rugnummers, huisnummers, autonummers, leeftijden, data (15 juli of de vijftiende van de zevende of 15-07-2007)
Inhoud voor: groep 5 en 6
als groep 3/4 +
- digitale kloktijden lezen en hanteren: zoals 21:34 uur
- breuk als maatgetal: stroken van , etc.
- breuken en kommagetallen als maatgetal in prijzen, maten en gewichten
- breuk als operator: 3/4 nemen van een strook of een aantal
- breuk als verhoudingsgetal, zoals in recepten
- vanuit een deel het geheel berekenen
- niet evenredige verhoudingen, zoals bij: een vierkant wordt vier keer zo groot als de zijden twee keer zo groot worden
Inhoud voor: groep 7 en 8
als in groep 5/6 +
- verhoudingsgetallen voor bijvoorbeeld: snelheid (50 km / uur), 30% (30 van elke 100), 3/5 (drie van elke vijf) en in vijfden verdelen en er drie nemen)
- het verschil tussen 3,5 meter en 3,50 meter
- verband leggen tussen breuken en delen
- relaties tussen percentages als 50%, 25%, 10%, 5%
- relatie tussen breuken en procenten (voor uitrekenen van percentages)
- percentages als verhoudingsgetallen, in verhoudingstabel, sectordiagram, stroken
- percentage als 1/100
- verhoudingen bij: toename en afname, stijging / daling, rente, winst, verlies, korting
- inzicht in lineaire en niet-lineaire maten, lineaire vergroting, oppervlaktevergroting, inhoudsvergroting
Toelichting: Aantallen of hoeveelheidgetallen
Getallen worden gebruikt om aantallen aan te geven.
Bijvoorbeeld:
- 3 kinderen
- 16.000.000 Nederlanders
- 45 boeken
Toelichting: Volgorde (plaats in een rij)
De telwoorden staan in een vaste volgorde, waarin elk getal een vaste plaats heeft. Die volgorde kan gebruikt worden om de plaats van iets in een rij aan te geven. Bijvoorbeeld:
- het derde kind in de rij;
- het vierde huis in de straat;
- de tweede prijs.
Toelichting: Hoeveelheden, groottes (maten) of tijd
Getallen worden gebruikt om maten weer te geven. In principe zegt een maatgetal hoe vaak een maateenheid in een grootte (of hoeveelheid) kan worden afgepast.
Bijvoorbeeld:
- er gaat 45 liter in de tank;
- er zit 450 gram jam in het potje;
- er gaan 24 uur in een dag;
- er kan 300.000 ton olie in de tanker.
Toelichting: Naamgetallen (en codes)
Voorbeelden van naamgetallen en codes zijn:
- de rugnummers bij voetballers;
- telefoonnummers en sofinummers, die enerzijds als naam; functioneren en anderzijds codering zijn;
- nummers van buslijnen en treinen.
Toelichting: Ankergetallen
Ankergetallen zijn getallen die belangrijk zijn door hun plaats in de telrij of door hun speciale getalstructuur: 1, 5, 10, 25, 50, 75, 100, ... Ze spelen een belangrijke rol bij het inzicht in de wereld van de getallen, het schattend en het handig rekenen, het afronden en bij het onderling verbinden van gehele getallen, kommagetallen en breuken. Bijvoorbeeld:
- Ordes van grootte:
- 1, 10, 100, 1.000, 10.000, 100.000, 1.000.000 en eventueel verder;
- 0,1, 0,01, 0,001, 0,000.1 en zo kleiner.
- Bijzondere getallen tussen ordes van grootte: tussen 10 en 100 bijvoorbeeld:
- 25, 50, 75, die op kwarten liggen;
- 20, 40, 60, 80 die op vijfden liggen, zoals bij het geld,
en eventueel
- 331/3 en 662/3 die op derden liggen.
- Deze zelfde soort ankergetallen heb je ook tussen 0 en 1, zoals bij:
- Getallen en breuken in verband met de klok:
- 1, 3, 6, 9, 12 en zo verder;
- 60 en 3600;
- de breuken 1/4, 1/2, 3/4.
- Getallen in verband met de kalender:
- aantallen dagen per jaar en per maand;
- veelvouden van 7 en zo verder.
- Belangrijke relaties zijn bijvoorbeeld:
- 1/2 = 0,5 = 50% = 1 op 2;
- 3/4 = 0,75 = 75% = 3 op 4;
- 1/3 = 0,333 = 33,3% = 1 op 3.
Toelichting: Referentiegetallen
Referentiegetallen zijn getallen die voor iemand speciaal bekend zijn en een bijzondere betekenis hebben. Bijvoorbeeld de eigen leeftijd, lengte, gewicht, huisnummer, maar ook het gewicht van een olifant, de snelheid van een jachtluipaard, het aantal inwoners van Nederland en de eigen woonplaats, de omvang van de Nederlandse begroting op Prinsjesdag of de afstand van de Aarde tot de zon. Ieder kind ontwikkelt zijn eigen collectie referentiegetallen.
Referentiegetallen zijn belangrijk bij het betekenis geven aan getallen: betekenis in de zin van "weet ik voorbeelden bij duizend of een miljoen?", maar ook betekenis in de zin van "waar gebruiken mensen getallen voor?".
Toelichting: Rekengetallen
In een rekenformule als 45 + 17 is het niet aan de orde of het om een volgorde, aantal of maat gaat. Wat belangrijk is, is de manier waarop je met deze getallen kunt rekenen. In het rekengetal staat de getalstructuur ( ..., honderdtallen, tientallen, eenheden, tienden, hondersten, ...) centraal.
Toelichting: Eigenschappen van de bewerkingen
Eigenschappen van de optelling
Bij optellen gaat het om samenvoegen of toevoegen van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van de optelling zijn bijvoorbeeld:
- de verwisseleigenschap van de optelling: 3 + 4 = 4 + 3
- de volgorde bij het optellen doet er niet toe: 8 + 6 = 8 + (2 + 4). Dat gebruik je bijvoorbeeld bij de splitsing bij de tien, 8 + (2 + 4) wordt dan (8 + 2) + 4 en dan doe je eerst 8 + 2 = 10 en dan 10 + 4 = 14
- 9 + 7 = 10 + 6 of 10 + 7 - 1 (ééntje méér, ééntje minder)
Eigenschappen van de aftrekking
Bij aftrekkingen gaat het om het verminderen of het bepalen van verschil van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van het aftrekken zijn bijvoorbeeld:
- een aftrekking mag je niet omkeren: 7 - 4 ≠ 4 - 7
- de volgorde doet er wel toe: (6 - 3) + 2 ≠ 6 - (3 + 2)
- 15 - 9 = 16 - 10 of 15 - 10 + 1 (ééntje meer, ééntje minder)
Eigenschappen van de vermenigvuldiging
Bij vermenigvuldigingen gaat het om herhalingen, zoals vier groepjes van 5, vier staafjes van 5, vier sprongen van 5. Of "vier keer (telkens) 5".
Belangrijke eigenschappen van het vermenigvuldigen zijn bijvoorbeeld:
- een vermenigvuldiging mag je verwisselen: 3 x 12 = 12 x 3
- de volgorde bij het vermenigvuldigen doet er niet toe: 6 x 24 = (2 x 3) x 24 = 2 x (3 x 24) = 2 x 72 = 144
- vermenigvuldigen met 10 is gemakkelijk: 10 x 256 = (256 tientallen) = 2560. Alles schuift een positie op, of kort gezegd: je zet er een nul achter.
- 6 x 99 = 6 x 100 - 6 x 1 (één keer meer, één keer minder)
- 8 x 25 = 4 x 50 (verdubbelen en halveren)
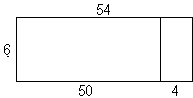
- de verdeeleigenschap: 6 x 54 = 6 x 50 + 6 x 4, zoals in het onderstaande oppervlaktemodel te zien is.
Eigenschappen van de deling
Bij verdelen kan het gaan om verdelen (Van een banketstaaf van 25 cm snijden we stukjes van 3 cm. Hoeveel stukjes kunnen we maken?) en opdelen (in een kring van vier kinderen delen we 20 kaartjes uit door telkens een rondje te geven. Hoeveel krijgt ieder?).
Belangrijke eigenschappen van het delen zijn bijvoorbeeld:
- een deling mag je niet omkeren: 12 : 3 ≠ 3 : 12
- bij een deling doet de volgorde er wel toe: (24 : 6) : 2 ≠ 24 : (6 : 2)
- delen door 10 is gemakkelijk. 2340 : 10 = (hoeveel tientallen zitten er in 2340) = 234. Je mag er een nul afhalen.
- bij een deling geldt ook de verdeeleigenschap: 64 : 4 = 40 : 4 + 24 : 4