Toelichting: Aantallen of hoeveelheidgetallen
Getallen worden gebruikt om aantallen aan te geven.
Bijvoorbeeld:
- 3 kinderen
- 16.000.000 Nederlanders
- 45 boeken
Toelichting: Volgorde (plaats in een rij)
De telwoorden staan in een vaste volgorde, waarin elk getal een vaste plaats heeft. Die volgorde kan gebruikt worden om de plaats van iets in een rij aan te geven. Bijvoorbeeld:
- het derde kind in de rij;
- het vierde huis in de straat;
- de tweede prijs.
Toelichting: Hoeveelheden, groottes (maten) of tijd
Getallen worden gebruikt om maten weer te geven. In principe zegt een maatgetal hoe vaak een maateenheid in een grootte (of hoeveelheid) kan worden afgepast.
Bijvoorbeeld:
- er gaat 45 liter in de tank;
- er zit 450 gram jam in het potje;
- er gaan 24 uur in een dag;
- er kan 300.000 ton olie in de tanker.
Toelichting: Naamgetallen (en codes)
Voorbeelden van naamgetallen en codes zijn:
- de rugnummers bij voetballers;
- telefoonnummers en sofinummers, die enerzijds als naam; functioneren en anderzijds codering zijn;
- nummers van buslijnen en treinen.
Toelichting: Ankergetallen
Ankergetallen zijn getallen die belangrijk zijn door hun plaats in de telrij of door hun speciale getalstructuur: 1, 5, 10, 25, 50, 75, 100, ... Ze spelen een belangrijke rol bij het inzicht in de wereld van de getallen, het schattend en het handig rekenen, het afronden en bij het onderling verbinden van gehele getallen, kommagetallen en breuken. Bijvoorbeeld:
- Ordes van grootte:
- 1, 10, 100, 1.000, 10.000, 100.000, 1.000.000 en eventueel verder;
- 0,1, 0,01, 0,001, 0,000.1 en zo kleiner.
- Bijzondere getallen tussen ordes van grootte: tussen 10 en 100 bijvoorbeeld:
- 25, 50, 75, die op kwarten liggen;
- 20, 40, 60, 80 die op vijfden liggen, zoals bij het geld,
en eventueel - 331/3 en 662/3 die op derden liggen.
- Deze zelfde soort ankergetallen heb je ook tussen 0 en 1, zoals bij:
- 0,25 - 0,5 - 0,75.
- Getallen en breuken in verband met de klok:
- 1, 3, 6, 9, 12 en zo verder;
- 60 en 3600;
- de breuken 1/4, 1/2, 3/4.
- Getallen in verband met de kalender:
- aantallen dagen per jaar en per maand;
- veelvouden van 7 en zo verder.
- Belangrijke relaties zijn bijvoorbeeld:
- 1/2 = 0,5 = 50% = 1 op 2;
- 3/4 = 0,75 = 75% = 3 op 4;
- 1/3 = 0,333 = 33,3% = 1 op 3.
Toelichting: Referentiegetallen
Referentiegetallen zijn getallen die voor iemand speciaal bekend zijn en een bijzondere betekenis hebben. Bijvoorbeeld de eigen leeftijd, lengte, gewicht, huisnummer, maar ook het gewicht van een olifant, de snelheid van een jachtluipaard, het aantal inwoners van Nederland en de eigen woonplaats, de omvang van de Nederlandse begroting op Prinsjesdag of de afstand van de Aarde tot de zon. Ieder kind ontwikkelt zijn eigen collectie referentiegetallen.
Referentiegetallen zijn belangrijk bij het betekenis geven aan getallen: betekenis in de zin van "weet ik voorbeelden bij duizend of een miljoen?", maar ook betekenis in de zin van "waar gebruiken mensen getallen voor?".
Toelichting: Rekengetallen
In een rekenformule als 45 + 17 is het niet aan de orde of het om een volgorde, aantal of maat gaat. Wat belangrijk is, is de manier waarop je met deze getallen kunt rekenen. In het rekengetal staat de getalstructuur ( ..., honderdtallen, tientallen, eenheden, tienden, hondersten, ...) centraal.
Toelichting: Eigenschappen van de bewerkingen
Eigenschappen van de optelling
Bij optellen gaat het om samenvoegen of toevoegen van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van de optelling zijn bijvoorbeeld:
- de verwisseleigenschap van de optelling: 3 + 4 = 4 + 3
- de volgorde bij het optellen doet er niet toe: 8 + 6 = 8 + (2 + 4). Dat gebruik je bijvoorbeeld bij de splitsing bij de tien, 8 + (2 + 4) wordt dan (8 + 2) + 4 en dan doe je eerst 8 + 2 = 10 en dan 10 + 4 = 14
- 9 + 7 = 10 + 6 of 10 + 7 - 1 (ééntje méér, ééntje minder)
Eigenschappen van de aftrekking
Bij aftrekkingen gaat het om het verminderen of het bepalen van verschil van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van het aftrekken zijn bijvoorbeeld:
- een aftrekking mag je niet omkeren: 7 - 4 ≠ 4 - 7
- de volgorde doet er wel toe: (6 - 3) + 2 ≠ 6 - (3 + 2)
- 15 - 9 = 16 - 10 of 15 - 10 + 1 (ééntje meer, ééntje minder)
Eigenschappen van de vermenigvuldiging
Bij vermenigvuldigingen gaat het om herhalingen, zoals vier groepjes van 5, vier staafjes van 5, vier sprongen van 5. Of "vier keer (telkens) 5".
Belangrijke eigenschappen van het vermenigvuldigen zijn bijvoorbeeld:
- een vermenigvuldiging mag je verwisselen: 3 x 12 = 12 x 3
- de volgorde bij het vermenigvuldigen doet er niet toe: 6 x 24 = (2 x 3) x 24 = 2 x (3 x 24) = 2 x 72 = 144
- vermenigvuldigen met 10 is gemakkelijk: 10 x 256 = (256 tientallen) = 2560. Alles schuift een positie op, of kort gezegd: je zet er een nul achter.
- 6 x 99 = 6 x 100 - 6 x 1 (één keer meer, één keer minder)
- 8 x 25 = 4 x 50 (verdubbelen en halveren)
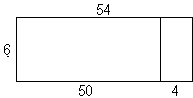
- de verdeeleigenschap: 6 x 54 = 6 x 50 + 6 x 4, zoals in het onderstaande oppervlaktemodel te zien is.
Eigenschappen van de deling
Bij verdelen kan het gaan om verdelen (Van een banketstaaf van 25 cm snijden we stukjes van 3 cm. Hoeveel stukjes kunnen we maken?) en opdelen (in een kring van vier kinderen delen we 20 kaartjes uit door telkens een rondje te geven. Hoeveel krijgt ieder?).
Belangrijke eigenschappen van het delen zijn bijvoorbeeld:
- een deling mag je niet omkeren: 12 : 3 ≠ 3 : 12
- bij een deling doet de volgorde er wel toe: (24 : 6) : 2 ≠ 24 : (6 : 2)
- delen door 10 is gemakkelijk. 2340 : 10 = (hoeveel tientallen zitten er in 2340) = 234. Je mag er een nul afhalen.
- bij een deling geldt ook de verdeeleigenschap: 64 : 4 = 40 : 4 + 24 : 4