Rekenen/wiskunde - Getallen en bewerkingen - kerndoel 26 - Groep 7 en 8 - Wat doet de leraar
De leerlingen leren structuur en samenhang van aantallen, gehele getallen, kommagetallen, breuken, procenten en verhoudingen op hoofdlijnen te doorzien en er in praktische situaties mee te rekenen.
Wat doet de leraar?
- De leraar laat kinderen zich verwonderen over getallen in diverse (extreme) contexten. Hiermee beoogt ze dat kinderen hun inzicht in getallen en maten verdiepen.
Een van de kinderen heeft het nieuwste 'Guinnessbook of records' mee naar school genomen. Hierin staan allerlei extreme situaties en prestaties beschreven, zoals wereldrecords voor verspringen, hoogspringen, snelste dier, kleinste mens, grootst gebakken pizza, etc. Als dergelijke voorbeelden voorgelezen worden, merkt de leraar dat er ook veel kinderen zijn die zich niet verwonderen over de extreme getallen of prestaties. Ze beseft dat zij zich eigenlijk geen voorstelling kunnen maken van de getallen in de gegeven context met de gegeven maten. Daarom stelt ze voor dat de kinderen in twee- of drietallen een record uit het boek mogen kiezen en in de komende week enkele momenten tijd krijgen om samen aan de klas via een uitbeelding te laten zien of het record nu bijzonder is of niet, zoals: hoe ver is het record verspringen van 8,95 meter? Hoe groot is een pizza met een diameter van 37,4 meter? En de grootste worst ooit gemaakt is 151,89 meter. Is dat eigenlijk wel lang? Ze maken van hun bevindingen een presentatie voor de klas.
- Gedurende het groepswerk en de presentaties komen verschillende maten, omzettingen, het metriek stelsel aan de orde, als mede het nut en belang van kommagetallen en de vraag of je mag afronden in dit soort situaties. Er ontstaan gesprekken waarin begrip van maten en getallen wordt uitgediept.
- De rol van de leraar is verwondering oproepen, kinderen laten reageren en hun denken laten verwoorden. Ze stimuleert kinderen naar elkaar te laten luisteren. Ze zorgt dat betekenissen van getallen en (relatieve) grootte van getallen nadrukkelijk aan de orde komen.
- Het onderdeel procenten is voor alle kinderen van belang omdat ze percentages in het dagelijks leven veel tegenkomen. De leraar beseft echter dat rekenen met procenten van de kinderen nogal wat vaardigheid vereist. Bij de introductie van de begrippen 'percentage' en 'procent' sluit ze daarom aan bij herkenbare contexten voor kinderen en houdt in de vragen die ze stelt, rekening met de verschillende niveaus van de kinderen. Ze laat de kinderen vertellen in welke situaties ze percentages tegenkomen, laat zoeken in folders en kranten. In (heterogene) groepjes bespreken de kinderen wat zo'n getal met het symbool % betekent. Ze laat de kinderen hiervan een poster maken. Tijdens de besprekingen komt aan de orde wat hoge en wat lage percentages zijn, of percentages die gegeven worden gunstig of ongunstig zijn (korting; rente, kans op regen). Sommige kinderen weten hoe je kunt rekenen met percentages, zoals 50% en 10%. Vanuit deze situatie laat de leraar de kinderen die dat kunnen percentages berekenen en uitleggen hoe je dit doet. Andere (zwakkere) rekenaars gaan op zoek naar gebruik van percentages en interpreteren de uitkomsten van berekeningen. Ze stelt bij deze introductie geen rekenregels aan de orde.
- De kinderen hebben regels van afronden bij geldbedragen geleerd. Maar hoe zit het met de nauwkeurigheid van afronden als het gaat om grote getallen? De leraar stelt dit aan de orde met de bedoeling de kinderen over de (relatieve) grootte van hoeveelheden te laten nadenken.
- De leraar legt de kinderen enkele problemen voor en vraagt waar voor hen grenzen van afrondingen liggen en laat hen daarover in kleine groepjes discussiëren. Het gaat niet om correcte antwoorden, maar om de redeneringen die kinderen maken en reacties die ze op elkaar geven:
- Een dorp heeft 8559 inwoners... Hoe mag je dit afronden in een folder? Met 8000? 9000? Of moet je iets preciezer zijn: 8500 of 8600?
- In een stadion bij een popconcert zijn 35.000 mensen. Dat zijn er natuurlijk niet precies 35.000. Wat zou het kunnen zijn geweest? En wat niet? Welke grenzen zijn er volgens jou?
- Nederland heeft 16,5 miljoen inwoners. Wat zou het iets preciezer kunnen zijn?
- De leraar stelt nogmaals de gelijkwaardigheid van breuken aan de orde, als herhaling en verdieping. Dit doet ze op een manier waarbij ze rekening houdt met de verschillende niveaus van begrip en vaardigheid door eigen producties van kinderen te stimuleren. Nadat ze met de klas heeft besproken hoe je ook al weer breuken kunt vinden die even groot zijn als een half, laat ze de kinderen zelf nieuwe breuken zoeken. Ze doet dit volgens samenwerkend leren, waarbij de kinderen zelf breuken bedenken, uitleggen aan elkaar waarom de breuken juist zijn en samen op zoek gaan naar nieuwe en moeilijke breuken. Als vanzelf komen de regels van gelijkwaardigheid aan de orde. (zie doorkijkje)
- De leraar weet van sommige kinderen dat ze veel meer aankunnen dan de reguliere methode biedt. Zij heeft verrijkingsmateriaal voor deze kinderen in de klas liggen, waaruit ze activiteiten mogen kiezen. Een van de activiteiten is nadenken over bijzondere getallen als oneindig en pi.
- Zij stimuleert de kinderen uit te zoeken via werkbladen en via internet wat het getal 'pi' inhoudt, hoe de mens aan dit bijzondere getal is gekomen, hoe groot het is (en de verschillende ideeën hierover door de geschiedenis heen). Ze geeft de kinderen de opdracht een (begrijpelijke) presentatie voor de klas te maken/te houden over dit onderwerp.
- De leraar zorgt dat kinderen gelegenheid krijgen om na te denken over getallen, de grootte/waarde, betekenissen, relaties en eigenschappen van getallen. Dit doet ze door (conflict) situaties aan te bieden zoals hierboven zijn beschreven en door de nadruk te leggen op verwoorden van gedachten en uitleggen aan elkaar, een wezenlijk onderdeel van wiskunde. Daarbij krijgt ze ook zelf gelegenheid om te zien in hoeverre kinderen inzicht en vaardigheid hebben (ontwikkeld) op het gebied van getalbegrip.
- Ze zorgt er ook voor dat kinderen hun vaardigheden voldoende oefenen en onderhouden, zeker als de rekenmethode daartoe wellicht onvoldoende mogelijkheden biedt. Hierdoor voorkomt ze dat verworven kennis en vaardigheden wegzakken.
Toelichting: Aantallen of hoeveelheidgetallen
Getallen worden gebruikt om aantallen aan te geven.
Bijvoorbeeld:
- 3 kinderen
- 16.000.000 Nederlanders
- 45 boeken
Toelichting: Volgorde (plaats in een rij)
De telwoorden staan in een vaste volgorde, waarin elk getal een vaste plaats heeft. Die volgorde kan gebruikt worden om de plaats van iets in een rij aan te geven. Bijvoorbeeld:
- het derde kind in de rij;
- het vierde huis in de straat;
- de tweede prijs.
Toelichting: Hoeveelheden, groottes (maten) of tijd
Getallen worden gebruikt om maten weer te geven. In principe zegt een maatgetal hoe vaak een maateenheid in een grootte (of hoeveelheid) kan worden afgepast.
Bijvoorbeeld:
- er gaat 45 liter in de tank;
- er zit 450 gram jam in het potje;
- er gaan 24 uur in een dag;
- er kan 300.000 ton olie in de tanker.
Toelichting: Naamgetallen (en codes)
Voorbeelden van naamgetallen en codes zijn:
- de rugnummers bij voetballers;
- telefoonnummers en sofinummers, die enerzijds als naam; functioneren en anderzijds codering zijn;
- nummers van buslijnen en treinen.
Toelichting: Ankergetallen
Ankergetallen zijn getallen die belangrijk zijn door hun plaats in de telrij of door hun speciale getalstructuur: 1, 5, 10, 25, 50, 75, 100, ... Ze spelen een belangrijke rol bij het inzicht in de wereld van de getallen, het schattend en het handig rekenen, het afronden en bij het onderling verbinden van gehele getallen, kommagetallen en breuken. Bijvoorbeeld:
- Ordes van grootte:
- 1, 10, 100, 1.000, 10.000, 100.000, 1.000.000 en eventueel verder;
- 0,1, 0,01, 0,001, 0,000.1 en zo kleiner.
- Bijzondere getallen tussen ordes van grootte: tussen 10 en 100 bijvoorbeeld:
- 25, 50, 75, die op kwarten liggen;
- 20, 40, 60, 80 die op vijfden liggen, zoals bij het geld,
en eventueel
- 331/3 en 662/3 die op derden liggen.
- Deze zelfde soort ankergetallen heb je ook tussen 0 en 1, zoals bij:
- Getallen en breuken in verband met de klok:
- 1, 3, 6, 9, 12 en zo verder;
- 60 en 3600;
- de breuken 1/4, 1/2, 3/4.
- Getallen in verband met de kalender:
- aantallen dagen per jaar en per maand;
- veelvouden van 7 en zo verder.
- Belangrijke relaties zijn bijvoorbeeld:
- 1/2 = 0,5 = 50% = 1 op 2;
- 3/4 = 0,75 = 75% = 3 op 4;
- 1/3 = 0,333 = 33,3% = 1 op 3.
Toelichting: Referentiegetallen
Referentiegetallen zijn getallen die voor iemand speciaal bekend zijn en een bijzondere betekenis hebben. Bijvoorbeeld de eigen leeftijd, lengte, gewicht, huisnummer, maar ook het gewicht van een olifant, de snelheid van een jachtluipaard, het aantal inwoners van Nederland en de eigen woonplaats, de omvang van de Nederlandse begroting op Prinsjesdag of de afstand van de Aarde tot de zon. Ieder kind ontwikkelt zijn eigen collectie referentiegetallen.
Referentiegetallen zijn belangrijk bij het betekenis geven aan getallen: betekenis in de zin van "weet ik voorbeelden bij duizend of een miljoen?", maar ook betekenis in de zin van "waar gebruiken mensen getallen voor?".
Toelichting: Rekengetallen
In een rekenformule als 45 + 17 is het niet aan de orde of het om een volgorde, aantal of maat gaat. Wat belangrijk is, is de manier waarop je met deze getallen kunt rekenen. In het rekengetal staat de getalstructuur ( ..., honderdtallen, tientallen, eenheden, tienden, hondersten, ...) centraal.
Toelichting: Eigenschappen van de bewerkingen
Eigenschappen van de optelling
Bij optellen gaat het om samenvoegen of toevoegen van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van de optelling zijn bijvoorbeeld:
- de verwisseleigenschap van de optelling: 3 + 4 = 4 + 3
- de volgorde bij het optellen doet er niet toe: 8 + 6 = 8 + (2 + 4). Dat gebruik je bijvoorbeeld bij de splitsing bij de tien, 8 + (2 + 4) wordt dan (8 + 2) + 4 en dan doe je eerst 8 + 2 = 10 en dan 10 + 4 = 14
- 9 + 7 = 10 + 6 of 10 + 7 - 1 (ééntje méér, ééntje minder)
Eigenschappen van de aftrekking
Bij aftrekkingen gaat het om het verminderen of het bepalen van verschil van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van het aftrekken zijn bijvoorbeeld:
- een aftrekking mag je niet omkeren: 7 - 4 ≠ 4 - 7
- de volgorde doet er wel toe: (6 - 3) + 2 ≠ 6 - (3 + 2)
- 15 - 9 = 16 - 10 of 15 - 10 + 1 (ééntje meer, ééntje minder)
Eigenschappen van de vermenigvuldiging
Bij vermenigvuldigingen gaat het om herhalingen, zoals vier groepjes van 5, vier staafjes van 5, vier sprongen van 5. Of "vier keer (telkens) 5".
Belangrijke eigenschappen van het vermenigvuldigen zijn bijvoorbeeld:
- een vermenigvuldiging mag je verwisselen: 3 x 12 = 12 x 3
- de volgorde bij het vermenigvuldigen doet er niet toe: 6 x 24 = (2 x 3) x 24 = 2 x (3 x 24) = 2 x 72 = 144
- vermenigvuldigen met 10 is gemakkelijk: 10 x 256 = (256 tientallen) = 2560. Alles schuift een positie op, of kort gezegd: je zet er een nul achter.
- 6 x 99 = 6 x 100 - 6 x 1 (één keer meer, één keer minder)
- 8 x 25 = 4 x 50 (verdubbelen en halveren)
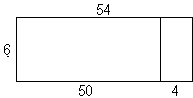
- de verdeeleigenschap: 6 x 54 = 6 x 50 + 6 x 4, zoals in het onderstaande oppervlaktemodel te zien is.
Eigenschappen van de deling
Bij verdelen kan het gaan om verdelen (Van een banketstaaf van 25 cm snijden we stukjes van 3 cm. Hoeveel stukjes kunnen we maken?) en opdelen (in een kring van vier kinderen delen we 20 kaartjes uit door telkens een rondje te geven. Hoeveel krijgt ieder?).
Belangrijke eigenschappen van het delen zijn bijvoorbeeld:
- een deling mag je niet omkeren: 12 : 3 ≠ 3 : 12
- bij een deling doet de volgorde er wel toe: (24 : 6) : 2 ≠ 24 : (6 : 2)
- delen door 10 is gemakkelijk. 2340 : 10 = (hoeveel tientallen zitten er in 2340) = 234. Je mag er een nul afhalen.
- bij een deling geldt ook de verdeeleigenschap: 64 : 4 = 40 : 4 + 24 : 4