Zoeken - zoekresultaten

Pantomime

De kinderen beelden zonder woorden gevoelens, handelingen en situaties uit.

Vertelpantomime

Tijdens een vertelling door de leraar beelden de kinderen de bijbehorende handelingen, gevoelens en situaties uit. Alle kinderen spelen tegelijkertijd, individueel of in tweetallen.

Rond een gegeven woord of attribuut laten de kinderen hun fantasie de vrije loop. Het ene woord kan het andere uitlokken: een wandelstok kan een bezem of strijkstok worden. Er zijn geen beperkende regels.

Bijvoorbeeld de vloeiende beweging van stromend water of de staccatobeweging van een robot. Deze bewegingen worden bepaald door op een bepaalde manier gebruik te maken van tijd kracht en ruimte.

Eibo = 'Engels in het basisonderwijs'. Het is verplicht vanaf groep 7. Er wordt ca. een uur per week aan Engels besteed, in 1 keer of over meerdere dagen verspreid.

Vervroegd Eibo = Engels start eerder dan groep 7. Er wordt ca. een uur besteed aan Engels per week.

Versterkt Eibo = enkele uren per week Engels in groep 7 en 8, bijvoorbeeld met het oog op internationale uitwisseling.

Extensief lezen = het lezen van (grotere) teksten waarbij de lezer niet ieder woorden hoeft te weten of te begrijpen, zoals bij het lezen van een boekje of een bladzijde uit een tijdschrift.

Intensief lezen = het lezen van korte teksten waarbij de lezer (bijna) ieder woord begrijpt.

Concentrisch werken = er is niet zozeer een opbouw in moeilijkheidsgraad maar een uitbouw met woorden, zinnen en vaardigheden per thema.

Fillers = woorden die je gebruikt om tijd te winnen om na te denken of om het gesprek gaande te houden, bijvoorbeeld: well, really, ofcourse, let me see.

In een veld van 9 bij 7 meter met twee eindvakken van een meter over de hele breedte proberen 2 partijen van 4 spelers een bal 4 keer over te spelen en daarna een speler in het eigen eindvak aan te spelen. De andere partij probeert de bal te onderscheppen. Er wordt gespeeld met de loopregel dat de balbezitter maximaal twee passen mag maken daarna een stuit en dan weer twee passen.

Woordtaal en beeldtaal zijn middelen om de objecten los van de context waarin je ze gebruikt weer te geven. Zinnen als "zesendertig is groter dan vierentwintig" of "Een vierkant kun je in twee driehoeken verdelen" kun je gebruiken om een wiskundige samenhang voor te stellen, zonder dat die een fysieke werkelijkheid beschrijft. Het gaat niet om de werkelijkheid, maar om de eigenschappen ("het zijn er 36") en de verbanden ("36 is groter dan 24", of: 36 > 24).

Eigenschappen van de optelling
Bij optellen gaat het om samenvoegen of toevoegen van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van de optelling zijn bijvoorbeeld:

• de verwisseleigenschap van de optelling: 3 + 4   =   4 + 3
• de volgorde bij het optellen doet er niet toe: 8 + 6   =   8 + (2 + 4). Dat gebruik je bijvoorbeeld bij de splitsing bij de tien, 8 + (2 + 4) wordt dan (8 + 2) + 4 en dan doe je eerst 8 + 2 = 10 en dan 10 + 4 = 14
• 9 + 7 = 10 + 6 of 10 + 7 - 1 (ééntje méér, ééntje minder)

Eigenschappen van de aftrekking
Bij aftrekkingen gaat het om het verminderen of het bepalen van verschil van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van het aftrekken zijn bijvoorbeeld:

• een aftrekking mag je niet omkeren: 7 - 4 ≠ 4 - 7
• de volgorde doet er wel toe: (6 - 3) + 2 ≠ 6 - (3 + 2)
• 15 - 9 = 16 - 10 of 15 - 10 + 1 (ééntje meer, ééntje minder)

Eigenschappen van de vermenigvuldiging
Bij vermenigvuldigingen gaat het om herhalingen, zoals vier groepjes van 5, vier staafjes van 5, vier sprongen van 5. Of "vier keer (telkens) 5".
Belangrijke eigenschappen van het vermenigvuldigen zijn bijvoorbeeld:

• een vermenigvuldiging mag je verwisselen: 3 x 12 = 12 x 3
• de volgorde bij het vermenigvuldigen doet er niet toe: 6 x 24 = (2 x 3) x 24 = 2 x (3 x 24) = 2 x 72 = 144
• vermenigvuldigen met 10 is gemakkelijk: 10 x 256 = (256 tientallen) = 2560. Alles schuift een positie op, of kort gezegd: je zet er een nul achter.
• 6 x 99 = 6 x 100 - 6 x 1 (één keer meer, één keer minder)
• 8 x 25 = 4 x 50 (verdubbelen en halveren)

• 

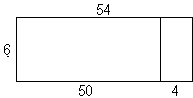
• de verdeeleigenschap: 6 x 54 = 6 x 50 + 6 x 4, zoals in het onderstaande oppervlaktemodel te zien is.

Eigenschappen van de deling
Bij verdelen kan het gaan om verdelen (Van een banketstaaf van 25 cm snijden we stukjes van 3 cm. Hoeveel stukjes kunnen we maken?) en opdelen (in een kring van vier kinderen delen we 20 kaartjes uit door telkens een rondje te geven. Hoeveel krijgt ieder?).
Belangrijke eigenschappen van het delen zijn bijvoorbeeld:

• een deling mag je niet omkeren: 12 : 3 ≠ 3 : 12
• bij een deling doet de volgorde er wel toe: (24 : 6) : 2 ≠ 24 : (6 : 2)
• delen door 10 is gemakkelijk. 2340 : 10 = (hoeveel tientallen zitten er in 2340) = 234. Je mag er een nul afhalen.
• bij een deling geldt ook de verdeeleigenschap: 64 : 4 = 40 : 4 + 24 : 4