Zoeken - zoekresultaten

Wiskundig inzicht en handelen

Kerndoel 23
De leerlingen leren wiskundetaal gebruiken.

Kerndoel 24
De leerlingen leren praktische en formele reken-wiskundige problemen op te lossen en redeneringen helder weer te geven.

Kerndoel 25
De leerlingen leren aanpakken bij het oplossen van reken wiskundeproblemen te onderbouwen en leren oplossingen te beoordelen.

Getallen en bewerkingen

Kerndoel 26
De leerlingen leren structuur en samenhang van aantallen, gehele getallen, kommagetallen, breuken, procenten en verhoudingen op hoofdlijnen te doorzien en er in praktische situaties mee te rekenen.

Kerndoel 27
De leerlingen leren de basisbewerkingen met gehele getallen in elk geval tot 100 snel uit het hoofd uitvoeren, waarbij optellen en aftrekken tot 20 en de tafels van buiten gekend zijn.

Kerndoel 28
De leerlingen leren schattend tellen en rekenen.

Kerndoel 29
De leerlingen leren handig optellen, aftrekken, vermenigvuldigen en delen.

Kerndoel 30
De leerlingen leren schriftelijk optellen, aftrekken, vermenigvuldigen en delen volgens meer of minder verkorte standaardprocedures.

Kerndoel 31
De leerlingen leren de rekenmachine met inzicht te gebruiken.

Meten en meetkunde

Kerndoel 32
De leerlingen leren eenvoudige meetkundige problemen op te lossen.

Kerndoel 33
De leerlingen leren meten en leren te rekenen met eenheden en maten, zoals bij tijd, geld, lengte, omtrek, oppervlakte, inhoud, gewicht, snelheid en temperatuur.

Kinderen leren om in allerlei situaties hoeveelheden, groottes, vormen, relaties en procedures ertussen te beschrijven. Daar gebruiken ze woorden bij, zoals telwoorden (drieënvijftig), maten (zeven en een halve meter), groter, kleiner, en dergelijke. Daarnaast gebruiken ze ook beeldtaal, zoals de getallenlijn, een rooster (tegelpleintje), pijlentaal en andere schematische weergaven om bijvoorbeeld structuur, verbanden of procedures weer te geven. Vooral grafieken en tabellen zijn bekende taalmiddelen om verbanden weer te geven. Bijvoorbeeld verbanden tussen 'prijs en aantal', of tussen 'afstand en tijd'. Bewerkingstekens en pijlentaal zijn geschikt om procedures weer te geven.

Basisberekeningen zijn berekeningen die je vlot en handig uit het hoofd kunt uitvoeren. In de praktijk gaat het vooral om berekeningen in het getalgebied tot 100:

• het optellen en aftrekken tot 100;
• het vermenigvuldigen en delen in het gebied tot 100,
  zoals 6 x 12 = 72 en 84 : 7 = 12;
• berekeningen boven de 100 die op basis van het rekenen met nullen direct te maken zijn, naar analogie van het rekenen tot 100
  zoals bijvoorbeeld:
  • het optellen en aftrekken van ronde getallen: 300 + 200 = 500, 700 - 200 = 500, 120 + 120 = 240;
  • vermenigvuldigen met ronde getallen: 6 x 200 = 1200, 800 : 4 = 200, 30 x 20 = 600.

Bij het schattend rekenen hoort ook inzicht in 'hoe ver je er naast zit' en hoe erg dat is. Leerlingen moeten leren dat 'ongeveer 321' in de meeste situaties een onzinnige uitspraak is. De uitspraak '1 + 1 is ongeveer 2' zal in de meeste gevallen als 'vreemd' worden bestempeld, terwijl '0,9 + 1,2 is ongeveer 2' wel degelijk van inzicht in getallen getuigt. De context en de bijbehorende bedoeling bepalen hoe nauwkeurig een schatting mag zijn. Een aardappelhandelaar en een apotheker zullen bij het afwegen van hun handel verschillend omgaan met nauwkeurigheid, al wijkt de acceptabele meetfout in percentages uitgedrukt, misschien niet eens zo heel erg van elkaar af.

Wie gaat behangen met rollen van 10 meter en muren heeft van 2,55m hoog, kan beter niet rekenen op basis van de schatting dat er ongeveer 4 banen (van 2,50 meter) uit een rol gaan. Deze geringe afronding heeft als effect is dat je niet genoeg behang koopt.
De context bepaalt welke afwijking bij schatten acceptabel is, en of afrondingen naar boven of naar beneden wenselijk zijn.
De vraag of 7258 op 7000 of op 7200 of op 7250 moet worden afgerond is zonder context niet te beantwoorden.

Over een evenwichtsbalk van ongeveer 2 meter lengte, 10 cm breed en 20 cm hoog lopen.

Over een evenwichtsbalk van ongeveer 3,5 meter lang en 6 cm breed schuin omhoog lopen (hoogte ongeveer 50 cm).

Over een evenwichtsbalk van ongeveer 3,5 meter lang en 6 cm breed schuin omhoog lopen naar een labiel punt (bijvoorbeeld aan een trapezestok van 1 meter hoog) met afstapplaats.

Extensief lezen = het lezen van (grotere) teksten waarbij de lezer niet ieder woorden hoeft te weten of te begrijpen, zoals bij het lezen van een boekje of een bladzijde uit een tijdschrift.

Intensief lezen = het lezen van korte teksten waarbij de lezer (bijna) ieder woord begrijpt.

Fillers = woorden die je gebruikt om tijd te winnen om na te denken of om het gesprek gaande te houden, bijvoorbeeld: well, really, ofcourse, let me see.

Eigenschappen van de optelling
Bij optellen gaat het om samenvoegen of toevoegen van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van de optelling zijn bijvoorbeeld:

• de verwisseleigenschap van de optelling: 3 + 4   =   4 + 3
• de volgorde bij het optellen doet er niet toe: 8 + 6   =   8 + (2 + 4). Dat gebruik je bijvoorbeeld bij de splitsing bij de tien, 8 + (2 + 4) wordt dan (8 + 2) + 4 en dan doe je eerst 8 + 2 = 10 en dan 10 + 4 = 14
• 9 + 7 = 10 + 6 of 10 + 7 - 1 (ééntje méér, ééntje minder)

Eigenschappen van de aftrekking
Bij aftrekkingen gaat het om het verminderen of het bepalen van verschil van aantalgetallen of maatgetallen.
Belangrijke eigenschappen van het aftrekken zijn bijvoorbeeld:

• een aftrekking mag je niet omkeren: 7 - 4 ≠ 4 - 7
• de volgorde doet er wel toe: (6 - 3) + 2 ≠ 6 - (3 + 2)
• 15 - 9 = 16 - 10 of 15 - 10 + 1 (ééntje meer, ééntje minder)

Eigenschappen van de vermenigvuldiging
Bij vermenigvuldigingen gaat het om herhalingen, zoals vier groepjes van 5, vier staafjes van 5, vier sprongen van 5. Of "vier keer (telkens) 5".
Belangrijke eigenschappen van het vermenigvuldigen zijn bijvoorbeeld:

• een vermenigvuldiging mag je verwisselen: 3 x 12 = 12 x 3
• de volgorde bij het vermenigvuldigen doet er niet toe: 6 x 24 = (2 x 3) x 24 = 2 x (3 x 24) = 2 x 72 = 144
• vermenigvuldigen met 10 is gemakkelijk: 10 x 256 = (256 tientallen) = 2560. Alles schuift een positie op, of kort gezegd: je zet er een nul achter.
• 6 x 99 = 6 x 100 - 6 x 1 (één keer meer, één keer minder)
• 8 x 25 = 4 x 50 (verdubbelen en halveren)

• 

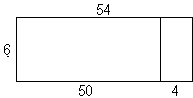
• de verdeeleigenschap: 6 x 54 = 6 x 50 + 6 x 4, zoals in het onderstaande oppervlaktemodel te zien is.

Eigenschappen van de deling
Bij verdelen kan het gaan om verdelen (Van een banketstaaf van 25 cm snijden we stukjes van 3 cm. Hoeveel stukjes kunnen we maken?) en opdelen (in een kring van vier kinderen delen we 20 kaartjes uit door telkens een rondje te geven. Hoeveel krijgt ieder?).
Belangrijke eigenschappen van het delen zijn bijvoorbeeld:

• een deling mag je niet omkeren: 12 : 3 ≠ 3 : 12
• bij een deling doet de volgorde er wel toe: (24 : 6) : 2 ≠ 24 : (6 : 2)
• delen door 10 is gemakkelijk. 2340 : 10 = (hoeveel tientallen zitten er in 2340) = 234. Je mag er een nul afhalen.
• bij een deling geldt ook de verdeeleigenschap: 64 : 4 = 40 : 4 + 24 : 4